0 := {} (the empty set)
N+1 := N 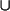 {N}
{N}
The von Neumann integers represent natural numbers and are constructed using the set notation. They are defined recursively as follows:
0 := {} (the empty set)
N+1 := N 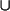 {N}
{N}
The smallest von Neumann integer zero is defined as the empty set. The von Neumann integer N is defined as the finite set with N elements which are the von Neumann integers 0 to N-1.
0 := {}
1 := 0 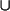 {0} = {0} = {{}}
2 := 1
{0} = {0} = {{}}
2 := 1 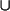 {1} = {0,1} = {{},{{}}}
3 := 2
{1} = {0,1} = {{},{{}}}
3 := 2 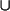 {2} = {0,1,2} = {{},{{}},{{},{{}}}}
{2} = {0,1,2} = {{},{{}},{{},{{}}}}
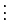 N+1 := N
N+1 := N 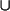 {N} = {0,1,2,...,N}
{N} = {0,1,2,...,N}
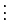
The set of von Neumann integers is infinite though every its element N is finite.
The von Neumann integer grows exponentially, for N>0 it has 5*2N-1-1 characters (braces and commas).
Check the von Neumann integer generator or the von Neumann integer test tool.